9020. Разбиение
на k подмассивов
Задан массив из n элементов
и число k. Разбейте этот массив на k подмассивов, используя все элементы исходного
массива (порядок элементов сохраняется, каждый элемент должен входить ровно в
один подмассив).
Для каждого разбиения вычисляется
максимум сумм элементов всех k подмассивов. Необходимо провести разбиение
так, чтобы этот максимум оказался наименьшим возможным. Найдите это минимально
возможное значение.
Вход. Первая
строка содержит два целых числа n и k (1 ≤ k ≤ n ≤ 106).
Вторая строка содержит n натуральных
чисел – элементы массива. Каждое число не
превышает 109.
Выход. Выведите
наименьшее возможное значение максимальной суммы среди всех допустимых
разбиений массива на k подмассивов.
Пояснение.
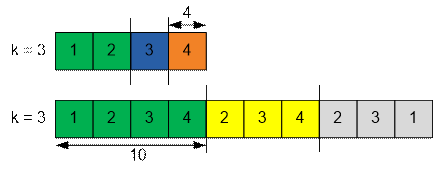
Для первого примера оптимальным разбиением будет {1, 2}, {3}, {4}. Суммы
подмассивов: 3, 3, 4. Максимум среди них – 4, и это наименьшее
возможное значение для k = 3.
Для
второго примера оптимальным разбиением будет {1, 2, 3, 4}, {2, 3, 4}, {2, 3, 1}. Суммы
подмассивов: 10, 9, 6. Максимум равен 10 – это наименьшее
возможное значение для k = 3.
|
Пример
входа 1 |
Пример
выхода 1 |
|
4
3 1
2 3 4 |
4 |
|
|
|
|
Пример
входа 2 |
Пример
выхода 2 |
|
10
3 1
2 3 4 2 3 4 2 3 1 |
10 |
РЕШЕНИЕ
бинарный
поиск
Анализ алгоритма
Будем искать оптимальное значение
с помощью бинарного поиска. Очевидно, что оно не может быть меньше 1 (так как
числа в массиве натуральные) и не может превышать сумму всех элементов массива.
Установим границы: left = 1, right
= сумма всех чисел
массива. Тогда ответ гарантированно находится в диапазоне [left;
right].
Рассмотрим вспомогательную
подзадачу: можно ли разбить массив на k подмассивов так, чтобы
максимальная сумма среди всех k подмассивов не превышала заданного
значения s0. Если в
массиве есть хотя бы один элемент, превышающий s0, такое разбиение невозможно. В остальных случаях
будем последовательно формировать подмассивы с суммой элементов, не превышающей
s0. Если в результате
получится не более k подмассивов, то такое разбиение возможно.
Пример
Во втором примере рассмотрим
возможные разбиения массива на подмассивы при различных значениях s0:



Реализация алгоритма
Объявим
константу MAX = 106 и рабочий массив m.
#define MAX
1000000
int m[MAX];
Функция f
возвращает 1, если массив можно разбить на k подмассивов так, чтобы
максимальная сумма среди всех k подмассивов не превышала заданного
значения s0.
int f(long long s0)
{
long long sum = 0;
int cnt = 1;
for (int i = 0; i < n; i++)
{
Если какой-либо элемент массива
больше s0, то такое
разбиение невозможно.
if (m[i] > s0) return 0;
Вычисляем сумму текущего
подмассива.
sum += m[i];
Как только текущая сумма превышает
значение s0, увеличиваем
счётчик подмассивов cnt на 1 и начинаем накапливать сумму следующего
подмассива.
if (sum > s0)
{
sum = m[i];
cnt++;
}
}
Если массив можно разбить не
более чем на k подмассивов, значит, его можно разбить и ровно на k
(k ≤ n) подмассивов.
if (cnt <= k) return 1;
return 0;
}
Основная часть программы. Читаем
входные данные. В переменной right вычисляем
сумму всех элементов массива.
scanf("%d %d", &n, &k);
left
= 1; right = 0;
for (i = 0; i < n; i++)
{
scanf("%d", &m[i]);
right += m[i];
}
Искомое минимальное значение максимальной суммы подмассивов находится в
диапазоне [left; right]. Запускаем бинарный поиск на этом отрезке.
while (left < right)
{
mid = (left + right) / 2;
if (f(mid) == 1)
right = mid;
else
left = mid + 1;
}
Выводим ответ.
printf("%lld\n", left);